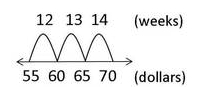
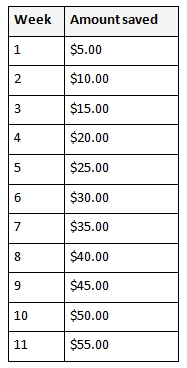
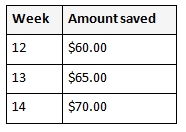
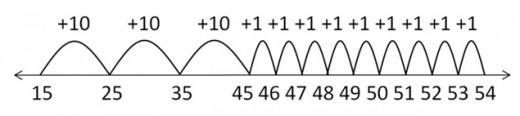
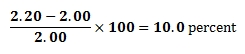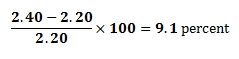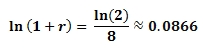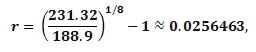All use of the Money as You Learn Web site, accessible at www.moneyasyoulearn.org, and related subdomains (collectively, the “Web site”) is subject to the following terms and conditions and our Privacy Policy all of which are deemed a part of and included within these terms and conditions (collectively, the “Terms”). By accessing the Web site you are acknowledging that you have read, understand, and agree to be bound by these Terms.
These Terms represent a binding contract between you and Money as You Learn (and any of their respective principals, officers, shareholders, members, employees or agents are herein collectively referred to as “Money as You Learn” or “we”). These Terms are in addition to any other agreements between you and Money as You Learn. If you do not agree with any of these terms and conditions, please do not use this Web site.
Money as You Learn reserves the right to change, modify, add or remove portions of these Terms at any time for any reason. Such changes shall be effective immediately upon posting. You acknowledge by accessing our Web site after we have posted changes to this Agreement that you are agreeing to these Terms as modified.
TRADEMARKS, COPYRIGHTS AND OTHER INTELLECTUAL PROPERTY
The content contained on the Web site is owned, licensed or otherwise lawfully used by Money as You Learn and is protected by applicable copyrights, trademarks, service marks, and/or other intellectual property rights. Money as You Learn hereby grants you access to its original content pursuant to a Creative Commons Attribution-Noncommercial-ShareAlike License, the terms of which are accessible at: http://creativecommons.org/licenses/by-nc-sa/3.0/legalcode. Money as You Learn hereby expressly reserves all rights not expressly granted in and to the Web site and its content.
Money as You Learn may post third-party content on the Web site. You are responsible for determining whether any such third-party content is protected by intellectual property rights, and for obtaining the appropriate permission from such third party. You shall be solely liable for any and all liability for any type of damages including, but not limited to, indirect, incidental, consequential or special damages, or losses or expenses, resulting from any infringement of any intellectual property rights, or any other harm resulting from, your input, distribution, uploading, posting, e-mailing, transmission or otherwise making available any content through the Web site.
USER CONDUCT
You may use the Web site for lawful purposes only. The Web site may not be accessed, reproduced, transmitted, or distributed without Money as You Learn’s permission. You may not commingle any portion of the Web site with any other information and may not edit, modify, or alter any portion of the Web site. In addition, you may not:
1. use or attempt to use any “scraper,” “robot,” “bot,” “spider,” “data mining,” “computer code” or any other automated device, program, tool, algorithm, process or methodology to access, acquire, copy, or monitor any portion of the Web site, any data or content found on or accessed through the Web site, or any other Money as You Learn information without prior express written consent of Money as You Learn;
2. obtain or attempt to obtain through any means, any materials or information on the Web site that has not been intentionally made publicly available either by public display on the Web site or through accessibility by a visible link on the Web site;
3. violate or work around any measure employed to limit or prevent access to the Web site or its content;
4. violate the security of the Web site or attempt to gain unauthorized access to the Web site, data, materials, information, computer systems or networks connected to any server associated with the Web site, through hacking, password mining or any other means;
5. impersonate any person or entity, or falsely state or otherwise represent an affiliation with a person or entity;
6. interfere with, attempt to interfere with or otherwise disrupt the proper working of the Web site, any activities conducted on or through the Web site or any servers or networks connected to the Web site, including accessing any data, content or other information prior to the time that it is intended to be available to the public on the Web site;
7. take or attempt to take any action that, in the sole discretion of Money as You Learn, imposes or may impose an unreasonable or disproportionately large load or burden on Money as You Learn or the infrastructure of the Web site; or
8. forge headers or otherwise manipulate identifiers in order to disguise the origin of any content you enter into the Web site.
USER CONTENT
You may not input, distribute, upload, post, e-mail, transmit or otherwise make available any content through the Web site that:
1. is promotional in nature, including solicitations for funds or business, or constitutes junk mail, spam, chain letters, pyramid schemes or the like, without the prior written authorization of Money as You Learn;
2. is unlawful, harmful, threatening, abusive, harassing, tortuous, defamatory, vulgar, obscene, libelous, invasive of another’s privacy, hateful, or racially, ethnically or otherwise objectionable;
3. you do not have the right to make available under any law or under contractual or fiduciary relationships (such as inside information, proprietary and confidential information learned or disclosed as part of employment relationships or under nondisclosure agreements);
4. contains software viruses or any other computer code, files or programs designed to interrupt, destroy or limit the functionality of any computer software or hardware, or telecommunications equipment;
5. is harmful to minors; or
6. constitutes personally identifiable information of any other person that such person has not authorized you to disclose.
CHILDREN UNDER 13
The Web site is not designed for children under the age of thirteen (13) and Money as You Learn does not intend to collect any personally-identifiable information from children under the age of 13. However, if children who are under 13 provide personally-identifiable information to us, their parents or legal guardian should request that we delete this information from our files by sending us an email at info@moneyasyoulearn.org. We will use all reasonable efforts to delete children’s information from our files.
MONITORING
Money as You Learn shall have the right, but not the obligation, to monitor the content of this Web site, including chat rooms, forums and comment areas, to determine compliance with these Terms and any operating rules or guidelines established by Money as You Learn, and to satisfy any law, regulation or authorized government request. Money as You Learn shall have the right, but not the obligation, to edit, refuse to post or remove any material submitted to or posted on this Web site. Without limiting the foregoing, Money as You Learn shall have the right to remove any material that Money as You Learn, in its sole discretion, finds to be in violation of the provisions hereof or otherwise objectionable.
INDEMNIFICATION
You agree to indemnify Money as You Learn from all damages, liabilities, costs, charges and expenses, including reasonable attorneys’ fees, which Money as You Learn may incur as a result of either: (i) your breach of these Terms; or (ii) content that you input, distribute, upload, post, e-mail, transmit or otherwise make available through Money as You Learn. Money as You Learn reserves the right, in its sole discretion, to assume the exclusive defense and control of any such matter for which you have agreed to indemnify Money as You Learn, in which event you shall have no further obligation to indemnify with respect to that particular matter.
DISCLAIMER
The information and materials provided on this Web site are general in nature and are not to be considered the rendering of legal, tax, accounting, financial, investment, insurance or other professional advice. If you require such advice or services, you should consult a qualified advisor. Individual considerations must be taken into account, and before making any specific decisions, you should consult a qualified professional. Decisions based on information contained on this Web site are your sole responsibility. While we welcome your active participation in the Web site, please note that we may not respond to all questions or requests for advice, and does not commit to responding within any particular period of time.
Some of our pages provide links to other Web sites. These Web sites are operated by independent third-party entities, and Money as You Learn is not responsible for the products or services offered or the information contained on these Web sites. The inclusion of any such links on our pages shall not constitute an endorsement of, or representation or warranty by, Money as You Learn regarding such Web sites, the content of such Web sites, the products or services of such Web sites, or the operators of such Web sites.
MONEY AS YOU LEARN HEREBY DISCLAIMS ANY AND ALL LIABILITY FOR ANY INFORMATION, MATERIALS, PRODUCTS OR SERVICES POSTED OR OFFERED AT ANY WEB SITE TO WHICH OUR WEB SITE LINKS. THE INFORMATION AND MATERIALS PROVIDED ON THIS WEB SITE, INCLUDING TEXT, GRAPHICS, LINKS OR OTHER ITEMS, ARE PROVIDED WITHOUT WARRANTY OF ANY KIND, EXPRESS, IMPLIED OR STATUTORY, INCLUDING, BUT NOT LIMITED TO, WARRANTIES OF PERFORMANCE, MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE, NON-INFRINGEMENT OF THIRD- PARTY RIGHTS AND FREEDOM FROM COMPUTER VIRUS. MONEY AS YOU LEARN DOES NOT WARRANT THE ACCURACY, ADEQUACY OR COMPLETENESS OF INFORMATION AND MATERIALS ON THIS WEB SITE AND EXPRESSLY DISCLAIMS ANY AND ALL LIABILITY FOR ERRORS OR OMISSIONS IN SUCH INFORMATION AND MATERIALS. MONEY AS YOU LEARN DOES NOT WARRANT THE UNINTERRUPTED AVAILABILITY OF THIS WEB SITE OR THE INFORMATION OR MATERIALS PROVIDED ON THIS WEB SITE.
TO THE EXTENT PERMITTED BY LAW, MONEY AS YOU LEARN HEREBY DISCLAIMS ANY AND ALL LIABILITY FOR ANY TYPE OF DAMAGES INCLUDING, BUT NOT LIMITED TO, INDIRECT, INCIDENTAL, CONSEQUENTIAL OR SPECIAL DAMAGES, OR LOSSES OR EXPENSES, IN EACH CASE ARISING FROM THE USE OR ATTEMPTED USE OF THIS WEB SITE, ANY INFORMATION OR MATERIALS PROVIDED ON THIS SITE OR ANY LINKED SITE, OR IN CONNECTION WITH ANY FAILURE OF PERFORMANCE, ERROR, OMISSION, INTERRUPTION, DEFECT, DELAY IN OPERATION OR TRANSMISSION, COMPUTER VIRUS, OR COMMUNICATION LINE OR SYSTEM FAILURE.
PRIVACY POLICY
To review the Money as You Learn Privacy Policy, click http://www.moneyasyoulearn.org/legal/privacy-policy
TERM AND TERMINATION
Money as You Learn shall have the right to immediately terminate your access to the Web site in the event of any breach by you of these Terms. Money as You Learn may discontinue or change this Web site, or its availability to you, at any time and for any reason.
GENERAL
The failure of Money as You Learn to insist upon strict compliance with these Terms shall not be construed as a waiver with regard to any subsequent failure to comply with such term or provision. You may not assign your rights or obligations under these Terms to anyone. If any provision in these Terms is invalid or unenforceable under applicable law, the remaining provisions will continue in full force and effect. These Terms shall be governed by the laws of the United States of America and the laws of the State of New York applicable to agreements made and to be performed entirely within such state, without regard to the conflict of law principles of such state. You hereby submit freely to the exclusive jurisdiction of the state and federal courts located in the Southern District of the State of New York and hereby irrevocably waive all defenses of lack of personal jurisdiction and forum non-conveniens.
Dated: April 15, 2013